eeet-222/1-16_Notes.md

Important info for lab

Input resistance

R_{in}=R_d(1+A\beta)

Gain

{V_o \over V_{in}}={A \over 1+A\beta}

output resistance

r_{out}={r_o\over 1+A\beta}

r_d is the resistance between the inputs.

r_o is the resistance on the output after the source.

The source within is represented as A_v(v_+-v_+)

{R_i \over R_i + R_f}=\beta is the feedback factor. \alpha={R_f\over R_i+R_f} is the control factor. A is the open-loop gain. (Closed-loop gain is when the output feeds back into the input)

R_i is the input resistor

R_f is the feedback resistor. It is ALWAYS back to the negative.

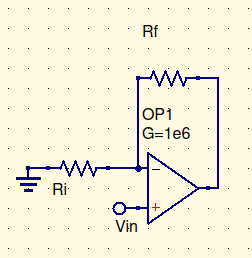
Simple feedback op-amp for examples

Gain

If A is finite, and r_d and r_o are neglected, then the gain = {R_i+R_f \over R_i}={1\over \beta}

Input resistance

goal\ r_{in}={1V\over I_{in}}\ .\ 0={v_-- 0\over R_i}+{v_-- V_{in}\over r_d}+{v_-- V_o\over R_f}\ i_{in}={1- V_- \over r_d}\ 0=V_-({R_iR_f+r_dR_f+r_dR_i \over R_ir_dR_f})-{1\over r_d}-{A(1-v_-) \over R_f}\ 0=V_-({(R_iR_f+r_dR_f+r_dR_i(1-A)) \over R_ir_dR_f})-{1\over r_d}-{A\over R_f}\ 1-i_{in}r_d=V_-\ 0=(1-i_{in}\cancel {r_d})({(R_iR_f+r_dR_f+r_dR_i(1-A)) \over R_i\cancel {r_d}R_f})-{1\over r_d}-{A\over R_f}\ 0=(1-i_{in})(1+{r_d\over R_i}+{r_d(1-A)\over R_f})-{1\over r_d}-{A\over R_f}\ 0=1-i_{in}+{r_d\over R_i}+{r_d(1-A)\over R_f}-{r_di_{in}\over R_i}-{r_d(1-A)i_{in}\over R_f}-{1\over r_d}-{A\over R_f}\ i_{in}(1+{r_d\over R_i}+{r_d(1-A)\over R_f})={r_d\over R_i}+{r_d(1-A)\over R_f}-{1\over r_d}-{A\over R_f}